Defiを理解しよう

このシリーズでは、有名どころのDefiプロダクトをなるべくわかりやすく解説していきたいと思います。

第1回目はCurve FinanceのStable Swapです。

基本的には下記のWhite Paperの内容をかみ砕いて解説したものになります。

StableSwap - efficient mechanism for Stablecoin liquidity

はじめに

Curve Finance

Curve Financeは2020年8月に正式ローンチされた、ステーブルコインに特化したDEX (Decentralized Exchange)です。

TVL（Total Value Locked）はDefiプロダクトの中で1位(2022年1月時点)であり、さまざまな他のDefiプロダクトに利用されている、昨今のDefiの心臓とも言えるプロダクトです。

今回はそのCurve Financeの基本中の基本とも言えるStable Swapの仕組みについて解説していきます。

Uniswap

Uniswapはv1が2018年11月にローンチされた最も老舗のDEXです。TVLではCurve Financeに劣りますが、取引高では現在(2022年1月時点)でも1位を誇っています。

SushiSwapなど数々のフォークを生み出した、DEXの始まりとも言えるプロダクトで、そのAMMの仕組みはイーサリアムチェーンだけでなく、他チェーンでも使用されています。

Curve Financeを理解するにはUniswapのAMMの知識も必須なため、UniswapのAMMの基礎も解説します。

Priceとは

まずはPriceとは何なのかということを理解しないとDEXの仕組みは理解できません。

Price X/Y とはXとYの交換比率のことです。

例えば、ETHの自動販売機があったとします。その自動販売機に２ETHを入れたとき、5000 USDが返ってきたとします。

そうすると、その自動販売機でのETH/USDのPriceは　5000 USD / 2 ETH = 2500 USDになります。

DEX, AMMとは

DEXとは仮想通貨の自動販売機です。

一般の取引所で行われているような板取引や販売所とは仕組みが違います。板取引は板注文を出す人が、販売所は取引所がPriceを決定しています。

それに対してDEXでは、その内部の仮想通貨のプールの量から自動でPriceを決めています。それがAMM（Automated Market Maker）です。

多くの人がDEXのプールからETHを引き出し、USDCを追加した場合（＝USDCを売り、ETHを買う）、ETHのプール量が少なくなりUSDCのプール量が多くなります。

その結果、ETH/USDCのpriceは上昇します。これが基本的な仕組みです。

Uniswap

UniswapのAMM

まずCurveの仕組みの前に、UniswapのAMMの仕組みを見ていきましょう。

UniswapのAMMのモデルでは、常に以下の式を満たすようにトークンが返却されます。

$x*y=k$

x,yはトークンX,Yのプールの量、kは定数です。

例えばxが100、yが100、プール内にあったとすると上記の式は

$x*y=100*100=10000$

となります。Uniswapのこのプールで、Xを10売ってみましょう。Yはいくら返ってくるでしょうか。

10を売却するので、売却後のXのプールの量は110となります。

上記の式を満たすようにYのプールの量が変動するため、。

$110 * y = 10000$

$y= 10000/110 = 90.909..$

となり、売却後のトークンYのプールの量は90.909となります。

priceは、(返ってきた量)/(売却した量)となるため

$100 - 90.909 = 9.09$

$y/x = 9.09 / 10 = 0.909$

この交換時のpriceは、0.909 となります。

交換前のpriceは1.000であったのに対し、交換した時のpriceが0.909と、9.1%のslippageが発生しました。

そしてこの交換後のpriceは 90.90 / 110 = 0.826 と、この取引によってpriceが下がったのがわかります。

これを一般化します。トークンXとYのプール量が y =f(x) で表されるプールにおいて、トークンXをa売却したとします。

その場合、返ってくるトークンYの量yとprice pは以下のように表せます。

$y = {f (x) - f(x + a)}$

$p = \frac {y} {a} = \frac {f (x) - f(x + a)} {a}$

例では10とプールに対して大きな量を売ったので、slippageが発生しました。

この売却量aが小さければ小さいほど現在のpriceに近づきます。

つまり、これは以下のようにf(x)の微分となり、priceはf(x)の接線の傾きとなります。

$- \lim_{a \to 0} \frac {f (x + a) - f(x)} {a}= - f'(x)$

UniswapのAMM グラフ

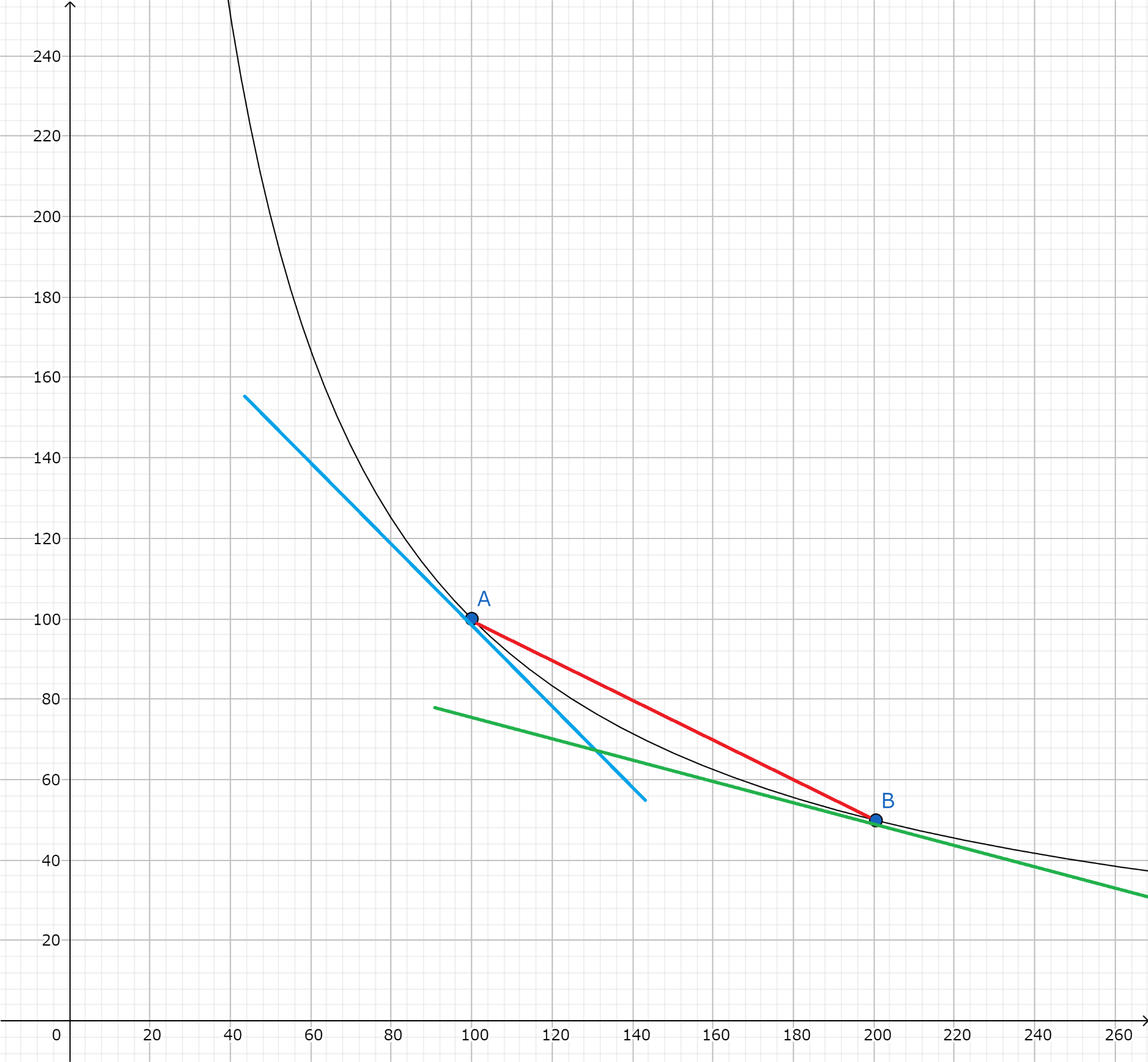
解りやすくするためにグラフで可視化してみましょう。以下の画像が x* y =100,000のグラフです。

プールがx=100,y=100のときのpriceは青線の点Aの接線の傾きになります。

そこからxを100売却したときのpriceは点Aと点Bを結んだ赤線の傾きになります。

そして売却後のpriceは緑線の点Bの接線の傾きになります。

slippageは青線の傾きと赤線の傾きの比率になります。

Xの量が多くなるにつれ、接線の傾きは平行に近づき、priceは0に収束します。

このUniswapの式では、プールが絶対に枯渇しません。

例ではトークンX,Yのプール量が(100,100)しかありませんが、この場合でもトークンXを100,000売ることができます。

Constant Swap

Constant SwapのAMM

UniswapのAMMのモデルは、ETHとUSDCのように価格が変動するものに対してよく動作します。

しかしUSDCとUSDTのように、いつもpriceが1:1になるようなステーブルコインのSwapに対してはどうでしょうか。

プール内のトークンの量に関わらずpriceは1を返したいはずです。

これを単純に実現するためには、以下の式を使うことができます。

$x+ y = k$

この式はCurve financeのWhite PaperではConstant Swapと呼ばれています。

Constant SwapのAMM グラフ

では、Uniswapの例のように、x=100,y=100のときの動きを見てみましょう。グラフは以下になります。

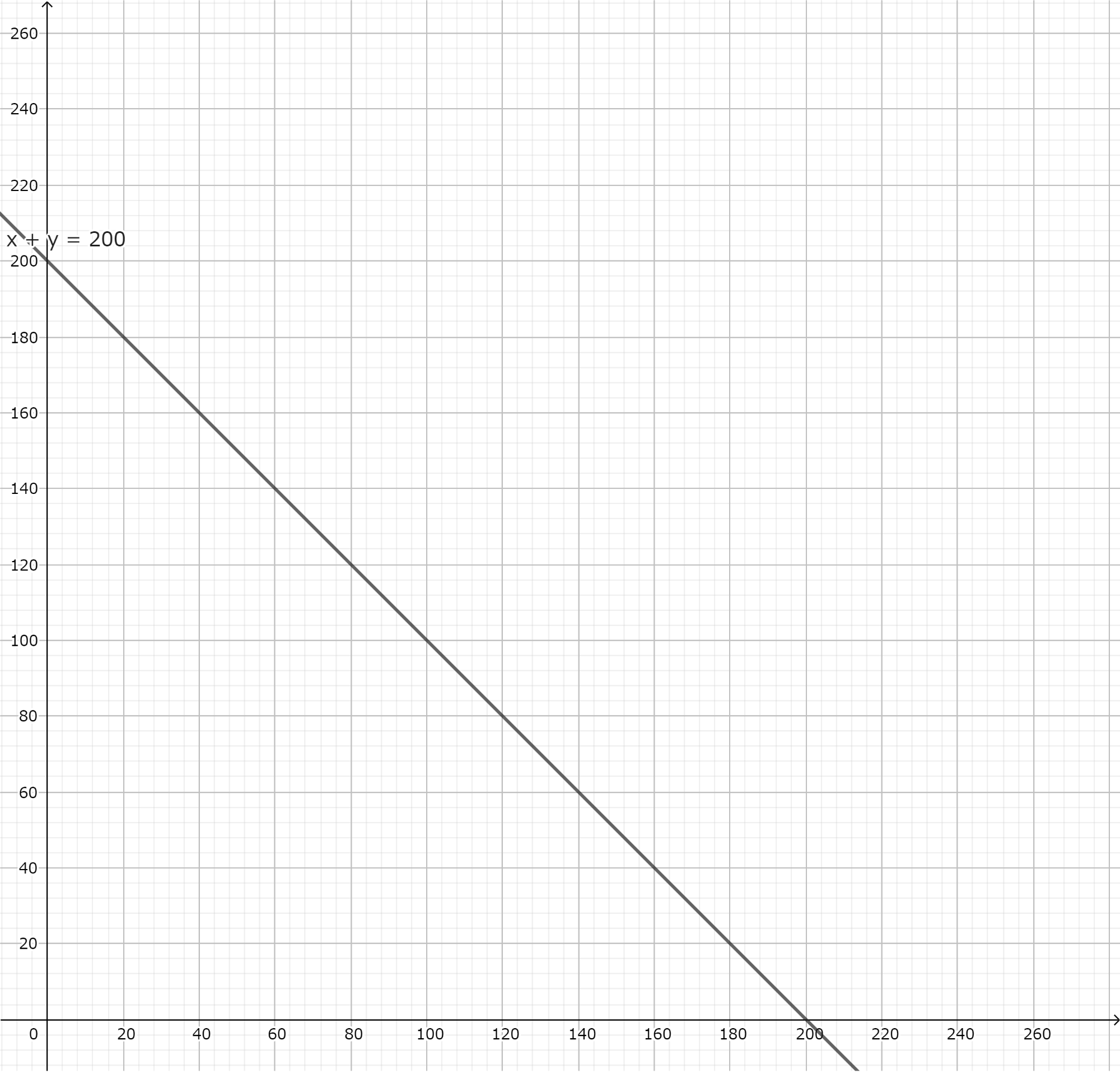
このConstant Swapのモデルでは、プールの量に関わらず常に一定の傾きとなり、Priceは常に1です。

しかし、グラフからわかる通り、xを100売却するとyのプール量が0となり枯渇します。

このConstant SwapではUniswapのときのようにトークンXは100以上売れません。

この問題を解決するにはどうすればいいでしょうか。

Curve Stable Swap

Stable SwapのAMM

Curve Financeが用いるAMMはStable Swapと呼ばれています。

一言で表現するならば、プールの量が均衡している（比率1:1）付近では x + y = kを、プールの量が偏っているときには x* y = kとなるような式を使用しています。

そのため、プールが枯渇せず、多少のプール量の増減に対してはpriceを1付近で安定させることができます。

このStable Swapの式を求めてみましょう。

そのために、まずはプールの量が均衡しているときの式を定義します。

xとyのプールの量が等しいときのそのプールの量の総和をDとして、Constant SwapとUniswapの式は下記の用に表現できます。

$x + y= D$

$x * y= (\frac {D} {2})^2$

次にUniswapの式とConstant Swapの式を足し合わせます。

ここで上記２式の比率を調整するために、レバレッジλを導入します。

単純にレバレッジλを乗算するのではなく、λがプール内の次元（トークンの数）に依存しないように、下記のようにConstant Swapの両辺にλDを乗算します。

$\lambda D(x + y) = \lambda D^2$

この式とUniswapの式を足し合わせます。

$\lambda D(x + y) + xy = \lambda D^2 + (\frac {D} {2})^2$

まずは、この式のグラフを見てみましょう。

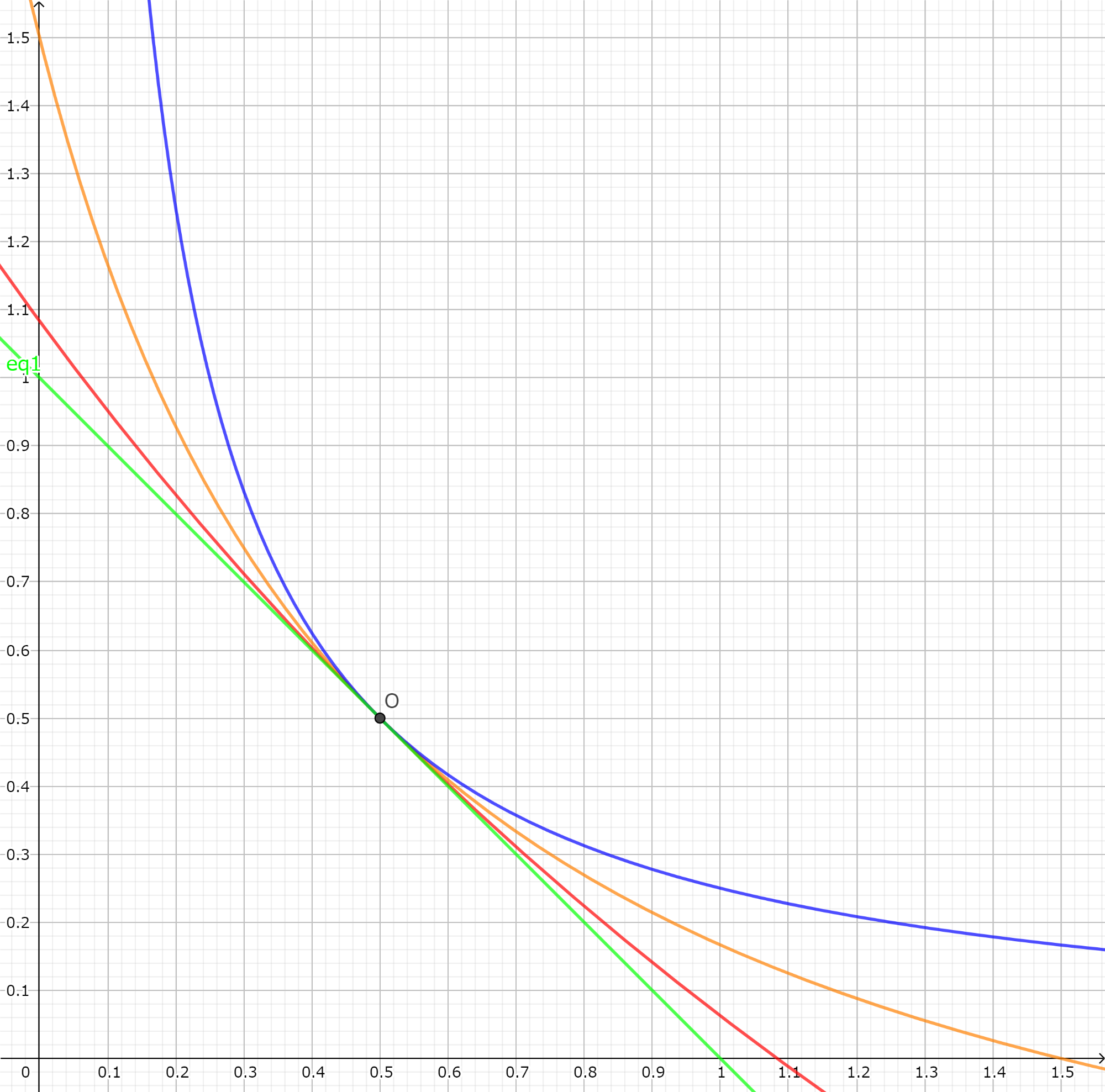
緑はD=1のConstant swapであり、青はUniswap, 赤はλ=3、橙はλ=0.5です。

λが小さくなるとUniswapと近い形になり、逆にλが大きくなるとConstant Swapに近づくことがわかります。

つまりこの式は、λが0のときUniswapモデルとして動作し、λが無限大のときはConstant Swapとして動作します。

この式は、プールが均衡している点O付近では使用することができます。

しかし、λが定数のままではy=0,x=0の点が存在し、いつかはプールが枯渇する状況が起きます。

理想的なλは、プールの量が均衡している時は定数、プールの量が偏るにつれて0となる動的なλ(x,y)である必要があります。

このλを求めることができれば、求めるStable SwapのAMMの式を導出することができます。

動的レバレッジ

そこでλを定数Aを用いて以下のように表現します。

$\lambda = A \frac {xy} {(\frac {D} {2})^2}$

xy を (D/2)^2で割るということは、プールの量が均衡状態からどれだけ偏っているかの比率を表しています。

つまり、プールの量が均衡しているときはxy=(D/2)^2となるので定数A、プールが極端に偏ったときはxy=0となるので、λ=0となります。

この定数Aは、Curve Financeのホワイトペーパーでは"amplification coefficient"(増幅係数)と呼んでいます。

このλを式に代入します。すると以下の式が導かれます。

$A \frac {xy} {(\frac {D} {2})^2} D (x + y) + xy = A \frac {xy} {(\frac {D} {2})^2} D^2 + (\frac {D} {2})^2$

この式を整理して、下記が導かれます。

$4A (x+y) +D = 4AD + \frac {D^3} {4xy}$

この式が、x,yの2つのプールでのCurve FinanceのStable Swapのモデルになります。

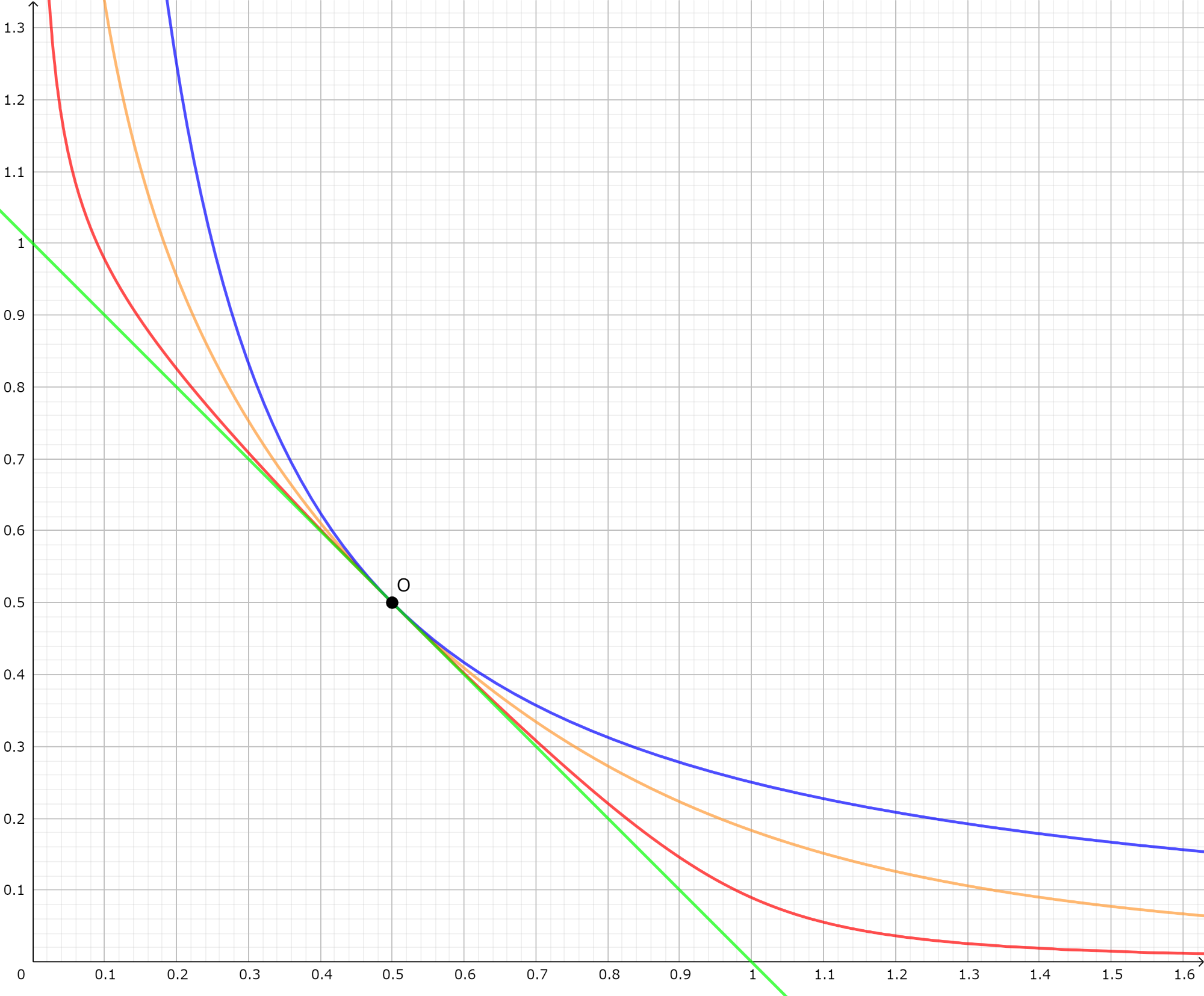
下記がこのStable Swapのグラフになります。

緑はD=1のConstant Swap、青はUniswap、赤はA=5のStable Swap、橙はA=0.5のStable Swapです。

増幅係数Aが大きくればConstant Swapに近づき、小さくなればUniswapに近づいていることがわかります。

λが定数の時とは違い、xが大きくなっても常にｙは0以上であることも見てとれます。

増幅係数A : amplification coefficient

ではこの増幅係数Aはどのように決定すればいいのでしょうか。

上記のグラフを拡大してみてみましょう。

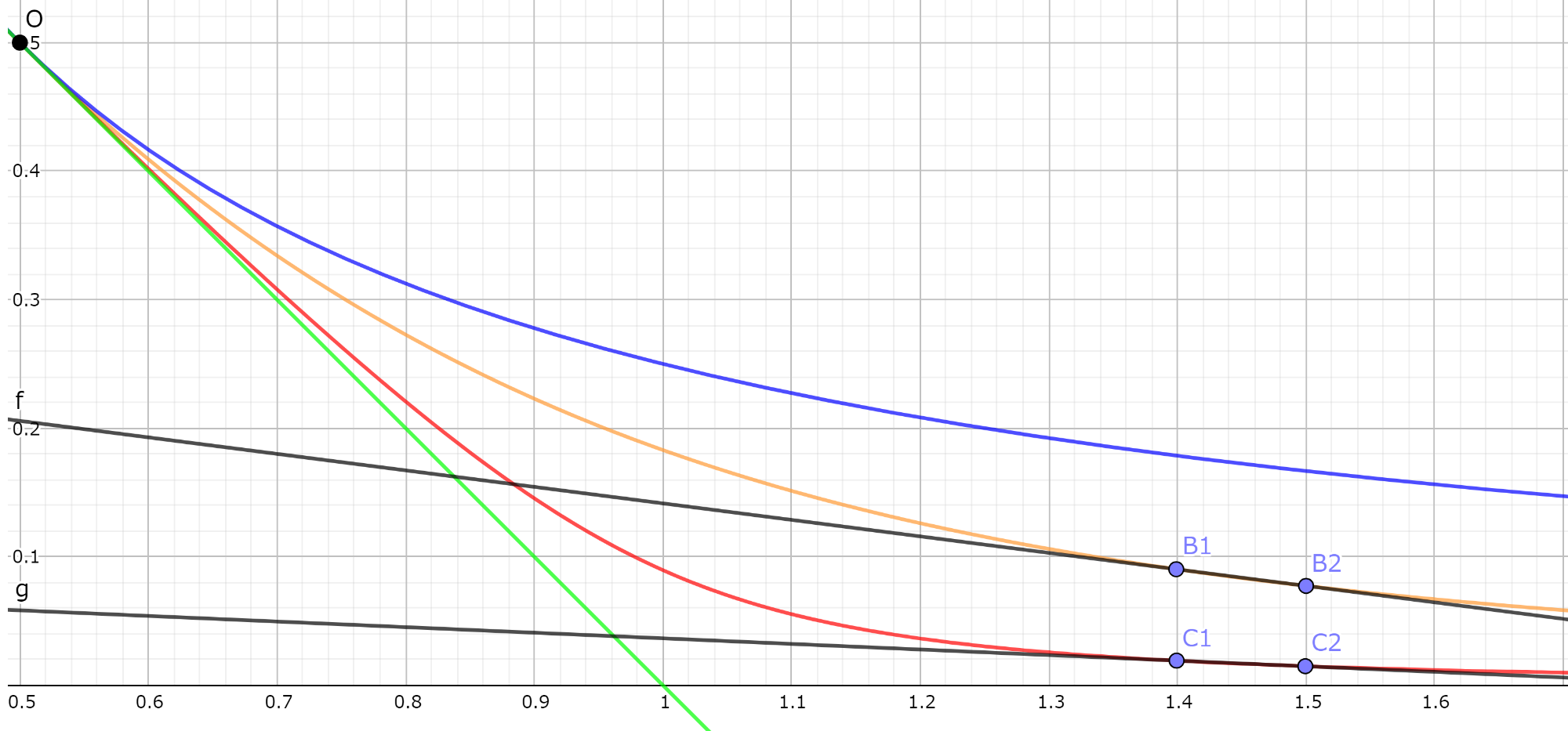
増幅係数Aが大きいほう（赤）が、均衡点O->C1では傾きが1に近いことがわかります。

つまりプールの量が均衡している状態では、増幅係数が大きいほうが価格が安定しています。

その一方、プールのバランスがくずれた点(B1,B2,C1,C2)に注目すると、赤C1-C2は橙B1-B2に比べ傾き小さく０に近くなっています。

これは増幅係数Aが大きいほうが価格の変動が激しくなっていることを意味します。

つまり増幅係数Aが大きいほうが、均衡点O付近では安定するが、プールのバランスが崩れてくるとpriceが急激に変化し不安定になります。

そのため、プール内のトークン量が安定し均衡するプールの増幅係数は大きくし、不安定で均衡しないプールでは増幅係数を小さくする必要があります。

この増幅係数の意思決定はveCRVを用いたDAOによって行われています。

増幅係数Aの変更の提案の例です。ここではLUSD poolのAを100から500に上げる提案を行っています。

基本的には新規でローンチしたプールのAは低く、安定するに従ってAを上げていく場合が多いようです。

Stable Swapのメリット

Curve FinanceのStable Swapは、Uniswapのプールの流動性にレバレッジをかけていることになります。

priceが1:1で安定するプールを作ろうと思うと、UniswapではStable Swapに比べ大量の流動性を供給する必要があります。

例えばトークンＸを10売却して、priceの変化を2%程度にしたい場合、UniswapではXとYのプールを売却量の少なくとも100倍ほど用意しなければなりません。

反面、Stable Swapでは増幅係数を大きくすることによってレバレッジをかけ、少ない量でプールを作ることができます。

ですので、価格が安定しているステーブルコインの流動性供給で非常に資本効率がよくなります。

しかし、ETH/USDCのように価格が安定することのないプールでは、価格の変動が非常に激しくなり不適です。

n個のトークンによる一般化

今回、単純化するために2つのトークンで説明しましたが、Curve Financeのwhite paperではn個のトークン（n次元）として計算しています。

n個のトークンの場合も基本的な計算は変わりません。

以下のように2次元のConstant SwapとUniswapの2つの式を次元nで置き換えます。

$\sum x_i = D$

$\prod x_i = (\frac D n)^n$

λD^(n-1)をConstant Swapの両辺に乗算します。

$\lambda D^{n-1}\sum x_i = \lambda D^n$

２次元のときと同様に両式を足し合わせます。

$\lambda D^{n-1}\sum x_i + \prod x_i = \lambda D^n + (\frac D n)^n$

動的なλはn次元の場合以下になります。

$\lambda = \frac {A\prod x_i} {(D/n)^n}$

λを代入して、以下の式を得ます。

$An^n \sum x_i + D = ADn^n + \frac {D^{n+1}}{n^n \prod x_i }$

上記の式がn次元のStable Swapの式になります。

まとめ

今回はCurve FinanceのStable Swapを解説しました。

Stable Swapの数式の意味が理解できたかと思います。

次回は、Curve Warとして話題のveCRV、DAOの解説をしたいと思います。