概要

Curve v2で導入されたDynamic feeについて解説します。簡単に言うと、プールがバランスした状態から乖離するにつれて手数料が高くなります。

序

Curve v2のホワイトペーパーでは、以下の $f$ の形でDynamic feeが与えられる、とあります:

$g=\frac{\gamma_{fee}}{\gamma_{fee}+1-\frac{\prod x_i}{(\sum x_i/N)^N}},$

$f=g\cdot f_{mid}+(1-g)\cdot f_{out}.$

これ以外に説明がなされていませんので、読者としては少し置いてけぼりな気分になるかもしれません。 一見難解に見えるこの項: $\prod x_i/(\sum x_i/N)^N$ さえ意味を掴めればなんとかなります。

相加平均と相乗平均

結論から先に言うと、$\prod x_i/(\sum x_i/N)^N$は相加平均と相乗平均の比率を表しています。アセット種類が2つ($x,y$)のときなら次のような形ですね:

$\begin{aligned} \frac{xy}{((x+y)/2)^2} \\\\ = \left(\frac{\sqrt{xy}}{(x+y)/2}\right)^2. \end{aligned}$

変形したら見たことのある形になったでしょうか?

相加平均と相乗平均の重要な関係は相乗平均 $\leq$ 相加平均です:

$\sqrt{xy} \leq \frac{x+y}{2}.$

これはN次元でも成り立ちます:

$\left(\prod x_i\right)^{1/N} \leq \left(\sum x_i\right)/N.$

等号が成り立つのは$x_i$が全て同じ場合です:

$x_1=\cdots =x_i=\cdots =x_N.$

つまり相乗平均/相加平均である例の項は必ず1以下になります:

$0 \lt\frac{\prod x_i}{(\sum x_i/N)^N} \leq 1, (x_i>0).$

なぜ相加/相乗平均が出てくるのか?

端的に言うと、Curveは以下の2つの式において $k$ を一定に保つという原理を組み合わせたAMMになっています:

$\begin{aligned} & x\cdot y=k, \\\\ & x+y=k. \end{aligned}$

下図の在庫曲線において、青線が $x\cdot y=k$ (Uniswap等)に対応し、赤線が $x+y=k$ に対応します。Curveはそれらの中間であるオレンジ線や緑線を表現することができます。 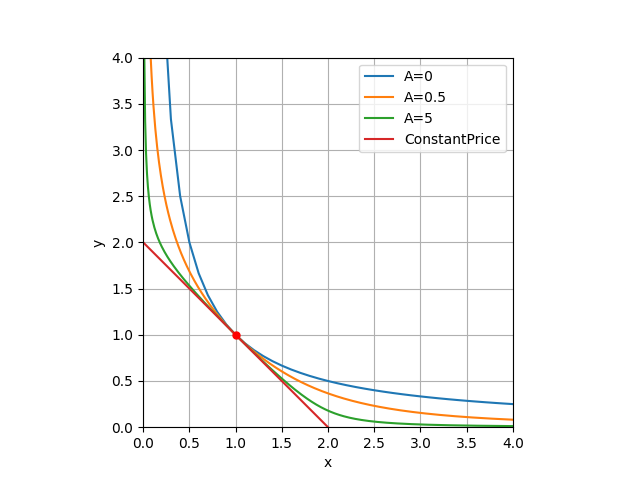このことの意味は以前解説したのでこちらの記事をご覧ください。 N次元で書くと次のようになります:

$\begin{aligned} & \left(\prod x_i \right)^{1/N} =k, \\\\ & \left(\sum x_i \right)/N=k. \end{aligned}$

つまるところ、相乗平均=一定と相加平均=一定の原理をブレンドしたのがCurveです。そしてそれらは $x=y$ のとき(上図赤点)に一致します。

Curve v1はステーブルコイン同士のプールだったので $x,y$ は在庫量と考えて良いですが、Curve v2はステーブルコインに限らないので、$x,y$を在庫の価値(=在庫量$\times$オラクル目標価格)と捉え直してください。

g因子のふるまい

$g$ は少し変形すると

$g=\frac{1}{1+\frac{1-\frac{\prod x_i}{(\sum x_i/N)^N}}{\gamma_{fee}}}$

です。

バランスしているとき

前々章で解説したように $\prod x_i/(\sum x_i/N)^N$ はプールがバランスしているときに最大値の1をとり、そのとき

$g=\frac{1}{1+\frac{1-1}{\gamma_{fee}}}=1$

となります。つまりそのとき $f=f_{mid}$です。

乖離しているとき

逆にバランス状態からひどく乖離して $\prod x_i/(\sum x_i/N)^N << 1$ となると

$g\sim \frac{1}{1+\frac{1}{\gamma_{fee}}}$

です。

TriCryptoPoolのコントラクトを見ると、fee_gamma=10000000000000000 となっており、$10^{-18}$をかけると0.01です。

そうすると

$g\sim \frac{1}{1+\frac{1}{\gamma_{fee}}}=0.0099\sim0.01$

なので、$f\sim f_{out}$ となります。

$\gamma_{fee}$ の意味

$\gamma_{fee}$ は変形した $g$ の分母に次の形で登場します:

$h=\frac{1-\frac{\prod x_i}{(\sum x_i/N)^N}}{\gamma_{fee}}.$

この分子はバランス状態からの乖離度を表しており、 $\gamma_{fee}$ はその乖離度をどの程度から深刻にとらえるかという尺度を与えています。例えばちょうど乖離度が $\gamma_{fee}$ くらいのときに

$h\sim1,$

$g\sim 1/2,$

$f\sim (f_{mid} + f_{out})/2$

となります。

乖離度($d$)を変数として $\gamma_{fee}=0.01$ のときの $g$ を図示すると以下のようになります。

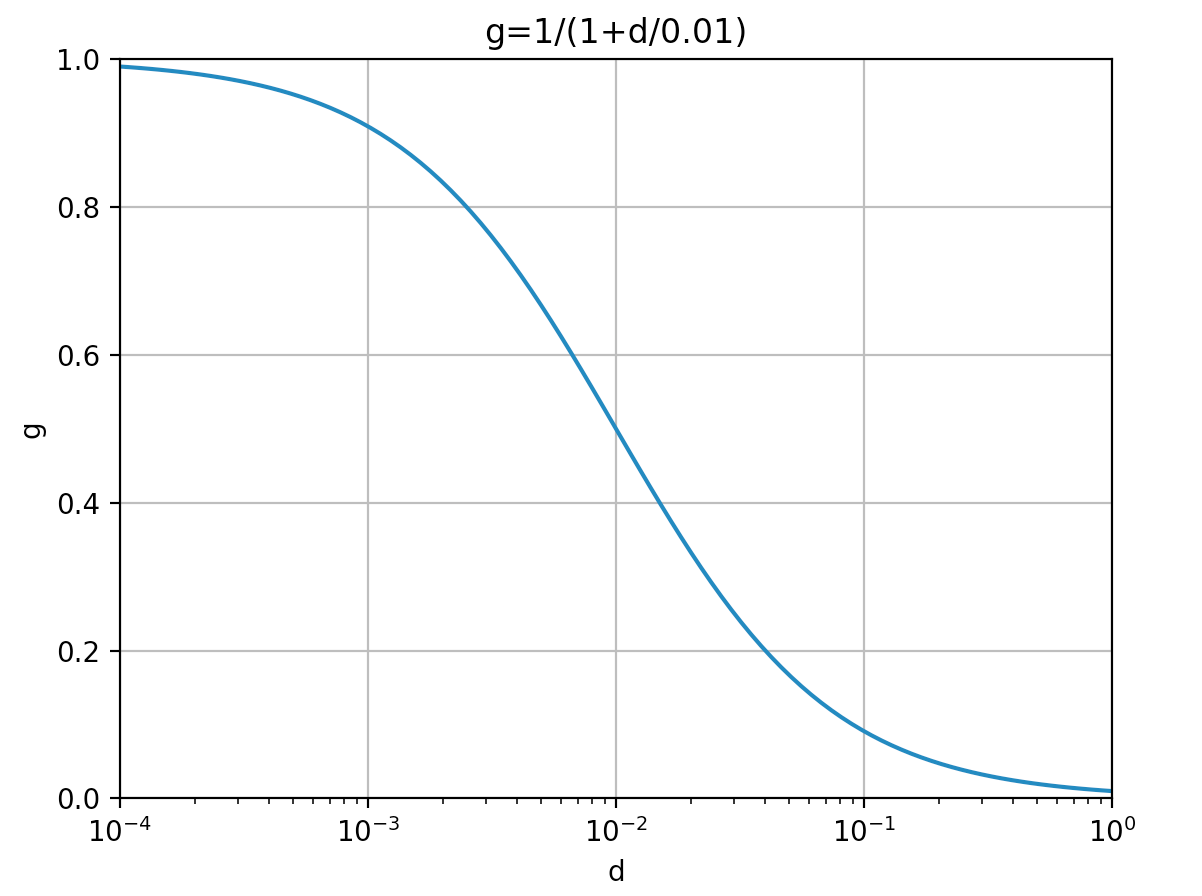
まとめ

以上、Curve v2のDynamic feeの解説でした。結論としては、相加平均と相乗平均の比率を使ってプールのバランス点からの乖離度を表現し、その比率に応じて最低手数料($f_{mid}$)から最大手数料($f_{out}$)までを接続させる仕組みになっていることがわかりました。また、$\gamma_{fee}$というパラメータにより乖離度に対して尺度が与えられていることもわかりました。

...と大体理解できたとは思うのですが、 TriCryptoPoolのコントラクトの mid_fee と out_fee の値は $10^{-18}$ をかけてみるとそれぞれ $4\times 10^{-12} , 4\times 10^{-11}$ となってとても小さいのが謎です。