Squeethを使ったUniswap v3のインパーマネントロスのヘッジ

最近、OpynはSqueethをデプロイしまし、Squeethを使ってUniswap v3のLPをヘッジする方法が公開されました "Hedging Uniswap v3 with SQUEETH"。SqueethはUSD/ETHの二乗をインデックスとしたトークンです。

前述の記事ではLPのヘッジであるために価格下落に対しては強固ですが価格上昇には機会損失を生んでいます。この記事ではSqueethを使ってインパーマネントロスをヘッジすることで流動性を提供した時の価格上昇に対して機会損失をカバーできることを見出しました。またこのヘッジをすることで下落した時でも流動性を提供するよりも損失をカバーできることを報告します。

*LPそのものをヘッジしていないのでLPのヘッジよりは下落に対して弱い

要約: インパーマネントロスの式をテイラー展開することで二次関数に近似することができました。この近似式を一階微分したΔは線形に、二階微分したΓは定数になります。Squeethも二次関数であるためΓは定数なのでヘッジができ、それぞれのΔを先物でヘッジすることができます。

Uniswap v3のインパーマネントロスの近似

インパーマネントロスは流動性トークンと現物を比べた際、価格が変化した時に現物をそのまま持っていた方がポートフォリオの資産額が高くなる、その損失のことを言う。

ポートフォリオをVとし、流動性トークンの価値をV_L, 現物の価値をV_kとすると、インパーマネントロスILは以下の式で示される。

$IL = V_L - V_k$

以前、Uniswap v3の流動性トークンの価値V_Lおよびdepositするときのそれぞれのトークンの量(x, y)を求めているため、以下のV_L, V_kからILを現在価格Pで表現することができる。

$x = \frac{L}{\sqrt{P}}- \frac{L}{\sqrt{P_M}}$

$y = L\sqrt{P} - L\sqrt{P_m}$

$L = \frac{y_0+P_i x_0}{2\sqrt{P_i}-\sqrt{P_m}-\frac{P_i}{\sqrt{P_M}}}$

$V_L = L(2\sqrt{P}-\sqrt{P_m}-\frac{P}{\sqrt{P_M}})$

$V_k = L(\sqrt{P_i}-\sqrt{P_m}+ \frac{P}{\sqrt{P}}- \frac{P}{\sqrt{P_M}})$

$IL(P) = L(2\sqrt{P}-\sqrt{P_m}-\frac{P}{\sqrt{P_M}}) - (L(\sqrt{P_i}-\sqrt{P_m}+ \frac{P}{\sqrt{P}}- \frac{P}{\sqrt{P_M}}))$

$= -\frac{L}{\sqrt{P_i}}(\sqrt{P}-\sqrt{P_i})^2$

P : 現在価格
P_i : depositしたときの価格
P_m : レンジの最低価格
P_M : レンジの最大価格
x₀ : depositするxの数
y₀ : depositするyの数
P_m ≦ P_i ≦ P_M
P_m ≦ P ≦ P_M

このILの式をPで2階微分する。

$IL'(P) = \frac{L}{\sqrt{P}} - \frac{L}{\sqrt{P_i}}$

$IL''(P) = -\frac{L}{2P^\frac{3}{2}}$

ここでILの式をP=aでテイラー展開すると以下のようになる。

$IL(P) = IL(a)+IL'(a)(P-a)+\frac{IL''(a)}{2!}(P-a)^2 + \omicron(P^3)$

a = P_i , ο(x³) = 0として近似した式をap.LP(P)とする。

$IL(P) \approx ap.IL(P) = -\frac{L}{4P_i^\frac{3}{2}}(P-P_i)^2$

以上、Uniswap v3のインパーマネントロスはテイラー展開によって二次関数に近似された。

Greekを求める

ap.IL(P)を二階微分してΔおよびΓを求める。

$\Delta = ap.IL'(P) = -\frac{L}{2P_i^\frac{3}{2}}(P-P_i)$

$\Gamma = ap.IL''(P) = -\frac{L}{2P_i^\frac{3}{2}}$

ヘッジを考える

SqueethはUSD/ETHの二乗をインデックスとしている。Squeethのポジションの損益およびそのΔ、Γは以下の式で表される。

$V = (\frac{P^2}{P_i^2}-1)P_i$

$\Delta = \frac{2P}{P_i}$

$\Gamma = \frac{2}{P_i}$

よってUniswap v3のインパーマネントロスのΔをヘッジするために必要なSqueethの量SQTHは以下の式で表される。

$SQTH = \frac{L}{2P_i^\frac{3}{2}} \div \frac{2}{P_i}= \frac{L}{4\sqrt{P_i}}$

このとき、Uniswap v3とSqueethから生じるΔの合計Dは以下のように表される。

$D = -\frac{L}{2P_i^\frac{3}{2}}(P-P_i)+ \frac{L}{4\sqrt{P_i}} \times\frac{2P}{P_i}$

$= \frac{L}{2\sqrt{P_i}}$

シミュレーション

今 1 ETH = $3000で1 ETHと3000 USDCをP_m = 1500, P_M = 6000のUniswap v3 プールにdepositすると考える。

それぞれをこれまでの式に代入していくと

$L = \frac{x+P_i y}{2\sqrt{P_i}-\sqrt{P_m}-\frac{P_i}{\sqrt{P_M}}}= 187.00$

$SQTH = \frac{L}{4\sqrt{P_i}} = 0.8535$

$\Sigma\Delta = \frac{L}{2\sqrt{P_i}} = 1.7071$

Squeethを0.8535 ETH 分ロング
ETH/USD先物を1.7071 ETH = $5121.3 分ショート

ポートフォリオは以下のように変化する。

USD/ETH ($)	変化率	Uniswap LP($)	LP分をHODLしていた場合($)	IL($)	Squeethの利益($)	先物の利益($)	ヘッジの合計($)
2400	-20%	5285.7	5400	-114.3	-921.8	1024.3	102.5
2700	-10%	5672.9	5700	27.1	-486.5	512.1	25.6
3000	0	6000	6000	0	0	0	0
3300	+10%	6275.5	6300	24.5	537.7	-512.1	25.6
3600	+20%	6506.5	6600	-93.5	1126.6	-1024.3	102.3

グラフで表現してみると以下のようになる。

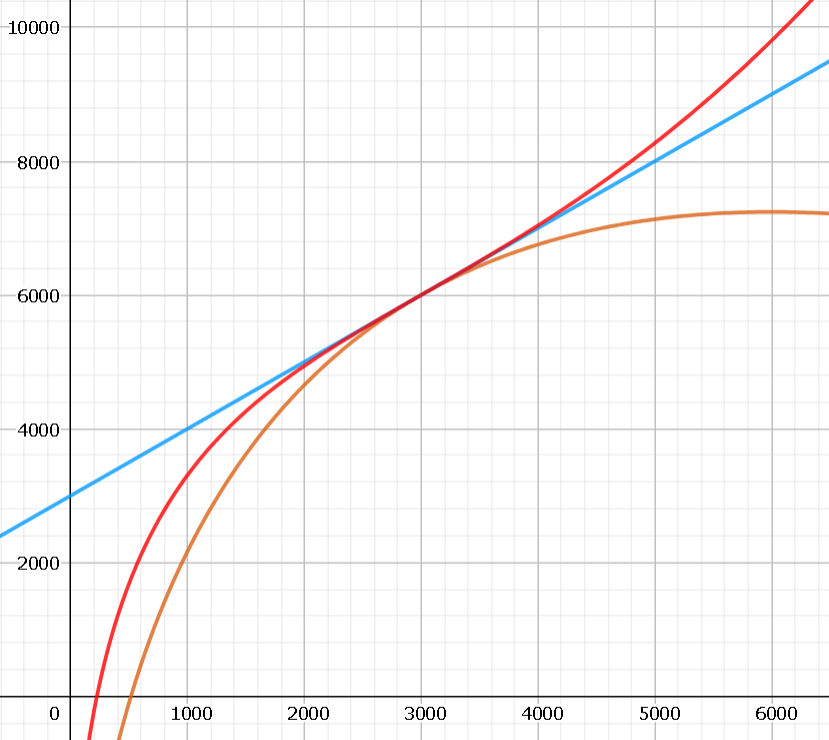青: HODL 赤: ILのヘッジ有黄: ILのヘッジ無

注意) このポジションはUniswapの手数料収入、SqueethのFunding Rate、先物の手数料を無視して作られている。そのため必ずしも一致しない。特にSqueethのFunding Rateは他の手数料収入よりも割高になっている。

Hedging Impermanent Loss of Uniswap v3 with SQUEETH

Recently, opyn deployed squeeth, and "Hedging Uniswap v3 with SQUEETH" was published. Squeeth is squared ETH index token.

Here, I show how to hedge the Impermanent Loss of Uniswap v3 with SQUEETH and futures.

TLDR: The IL is approximated as the quadratic curve using the Taylor series. So the Delta is approximated as the linear and the Gamma is approximated as the constant. Since SQUEETH's Gamma is constant, we can hedge the IL's Gamma with SQUEETH, and Delta is hedged by futures.