はじめまして。 solc(@solc_cyan)です。
HiÐΞで初投稿ですが、記事を書くこと自体ほぼ初めてようなものなので温かい目で読み進めていただければ嬉しいです。

この記事では最近話題の ゼロ知識証明 について高校数学の基礎くらいを前提知識として、「なんとなくわかる」を目標にして話していきたいと思っています。
厳密性を欠く表現が多くなると思いますが、この記事が厳密な議論をしている文献を読むための足掛かりになってくれれば幸いです。
私自身勉強中なので間違い等もあると思います。そういう時はそっと教えていただけると嬉しいです。

そもそもゼロ知識証明って何?

突然ですが皆さんはウォレットを持ってますか?HiÐΞを利用している方は持ってる方も多いと思います。
例えば0x82079567d9d67dfd93E96AE240b96cc03C645b58というアドレスのウォレットに100ETHが入っていたとします。私が「このウォレットは私のものだ!!」と知り合いのAさんに主張したいときどうすればいいでしょうか。\

そうです、とても簡単です。秘密鍵をAさんに見せてあげればいいのです。「ね、秘密鍵持ってるからこのウォレットは私の物でしょ。」となるわけです。はい、めでたしめでたし。

とはなりません。こんなことをしたら数分後には私の100ETHはどこかに消えているでしょう。
ではどうすればいいのでしょうか。私はAさんにウォレットは私のものだと証明したいのに秘密鍵を教えちゃダメという困った状況に置かれたわけです。

こうした問題を解決するために提案されたのがゼロ知識証明プロトコルです。
ゼロ知識証明はある命題uの証拠wを持っていることを相手に証拠wを持っているという情報以外を知られることなく証明するというものです。\

今回の場合だと「このウォレットは私のものだ！」という命題を私がAさんに証明した結果Aさんが知りうる情報は「ああ、確かにこれは君のものだ。」のみであるというような状況になります。もちろんAさんが証拠である秘密鍵を知ったりするようなことはありません。\

どうですか?ゼロ知識証明なんとなく凄そうな雰囲気がしてきませんか?

ゼロ知識証明プロトコルの持つ性質

ゼロ知識証明プロトコルは3つの性質を持ちます。この記事ではここ以降証明者Pさんと検証者Vさんの二人の登場人物が出てきます。

1.完全性(Completeness)

命題uに対してPさんが証拠wを持っているとき(Pさんが言ってることが本当だったら)Vさんは高確率でPさんが証拠wを持っているという主張が本当だとわかる。

2.健全性(Soundness)

命題uに対してPさんが証拠wを持っていないとき(Pさんが言ってることが嘘だったら)Vさんは無視できる小さい確率(ほぼ0%)を除いてPさんが証拠wを持っているという主張が嘘だとわかる。

3.ゼロ知識性(Zero Knowledge)

命題uに対してPさんが証拠wを持っているとき、Vさんが悪意を持っていて、証拠wを知ろうと試みても証拠wを知ることはできない。 (公開された情報のみから模倣した確率分布がVのもつ情報の確率分布と識別不可である。)

対話型ゼロ知識証明プロトコルを構成してみよう

こんなことばかり言われてもイメージがわかないと思うので実際に高校数学レベルの数学でゼロ知識証明プロトコルの具体例を構築してみたいと思います。

今回は以下のような状況を想像してみます。(ここでは$y$が与えられて$y=x^2$となる$x$を見つけることを難しい問題と仮定しています。)

「PさんとVさんが一緒にある自然数$y$が与えられ、それがどの数字の平方数なのかあてるゲームをしている。Pさんが$y=x^2(x,y\in\mathbb{N})$となる$x$を見つけたと主張した。」

ここでPさんが$y = x^2,(x,y\in\mathbb{N})$という式について$x$を知っているということをVさんに対して証明してみます。
この時、命題uは「$y=x^2$を満たす$x$が存在する」であり証拠wは「$x$」です。

当然ですが$x$をVさんに開示すればPさんが本当に$x$を知っているという証明になりますがそれではPさんが秘密にしたい情報$x$をVさんに知られてしまいます。ではどうすればいいでしょうか。

手順
①Pさんがランダムな要素$r(r \in \mathbb{Z}_q)$を生成して$a=r^2$を計算し、$a$をVさんに送る。
②Vさんが$b\in{0,1}$をランダムに生成し、$b$をPさんに送る。
③Pさんが送られてきた$b$を使って$c=x^br$を計算して$c$をVさんに送る。
④Vさんが$c^2=y^ba$が成立するか確認し、成立するとoutput = 1,不成立だとoutput=0を出力する。
⑤output = 0だとその時点で繰り返し終了。output = 1だと①に戻る。
この①~⑤をn回繰り返す。

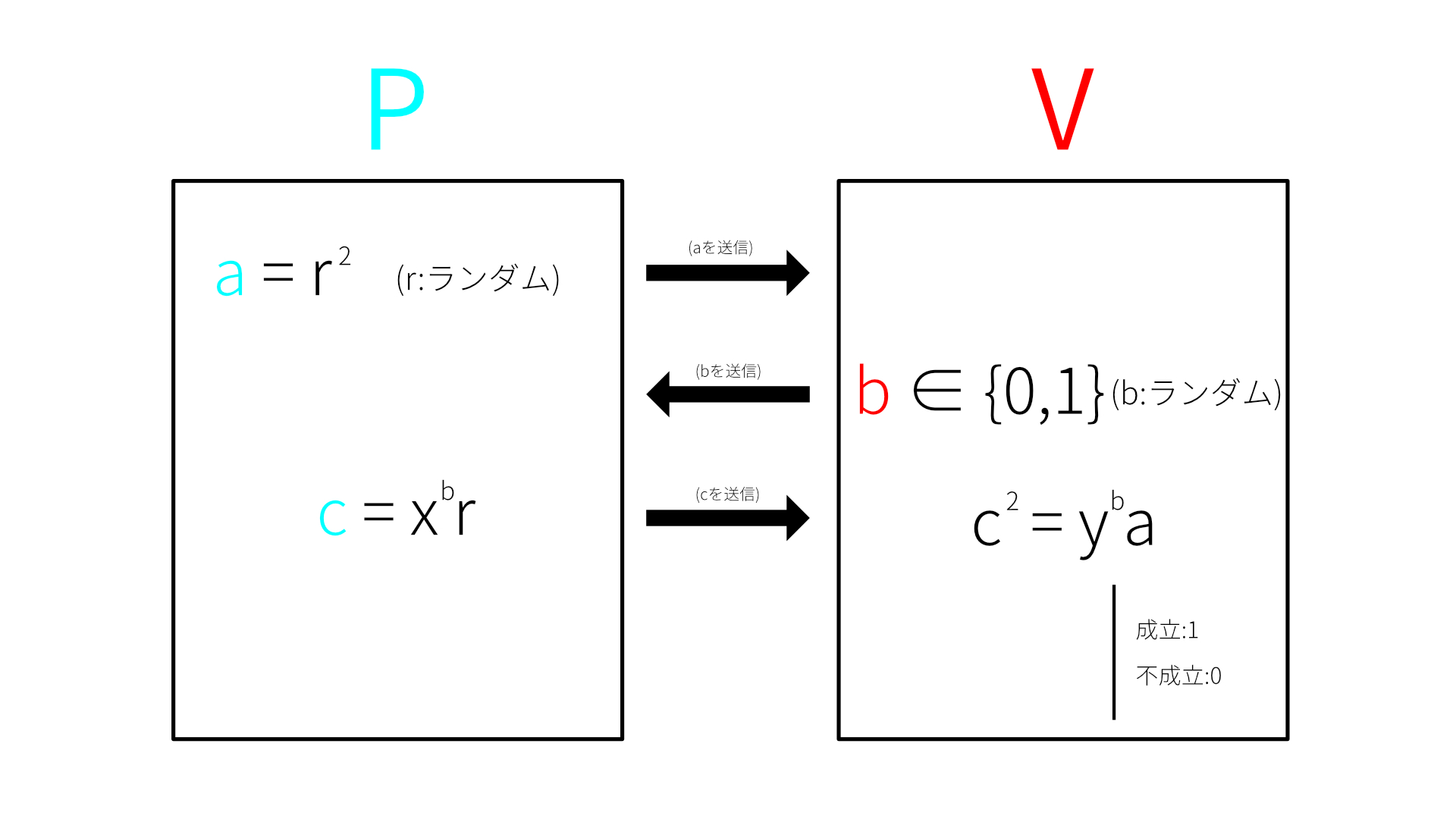
難しそうに見えますがやっていることはとても単純です。これがn回すべてでoutput=1ならVさんはPさんが$x$を知っているということを本当だと認めます。

ではこれが上記の性質を満たしていることを確認します。
1.完全性(Completeness)
Pが$x$を知っているとき、$b=0$でも$b=1$ でも確率1でoutput = 1となる。
2.健全性(Soundness)
Pが$x$を知らない時$b=0$ならoutput=1となるが$b=1$の時output=0となる。 n回すべてでoutput=1となる確率は$\left(\frac{1}{2}\right)^n$であり、$\displaystyle \lim_{n\rightarrow \infty} \left(\frac{1}{2}\right)^n =0$であるのでこれは無視できる小さい確率である。
3.ゼロ知識性(Zero Knowledge) (軽く読みとばしてください)
以下の手順でVの情報を模倣する。(n回目の繰り返し時)
①$R,b_n',c_n'$をランダムに定めたのち、$a_n'=\frac{{c_n'}^2}{y^{b_n'}}$を計算し、実際に返ってきた$b_n$がランダムに選んだ$b_n'$と一致すればそのまま操作を続ける。一致しなければ最初に戻る。
この模倣による確率分布は実際の手順を行った時の確率分布と完全に一致する。

こうして、これがこれが上記の性質を満たしていることを確認しました。(ゼロ知識性だけ説明する良い表現が思い浮かびませんでした。) このようにPさんとVさんが何度もやり取りを続けて行うゼロ知識証明プロトコルを対話型ゼロ知識証明プロトコルといいます。

おわりに

ここまで読んでくださってありがとうございました。気が向いたら非対話型の話やzk-SNARKsの話もしたいと思います。少しでも何かの参考になれば幸いです。

参考文献

The Knowledge Complexity of Interactive Proof-Systems
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.419.8132&rep=rep1&type=pdf